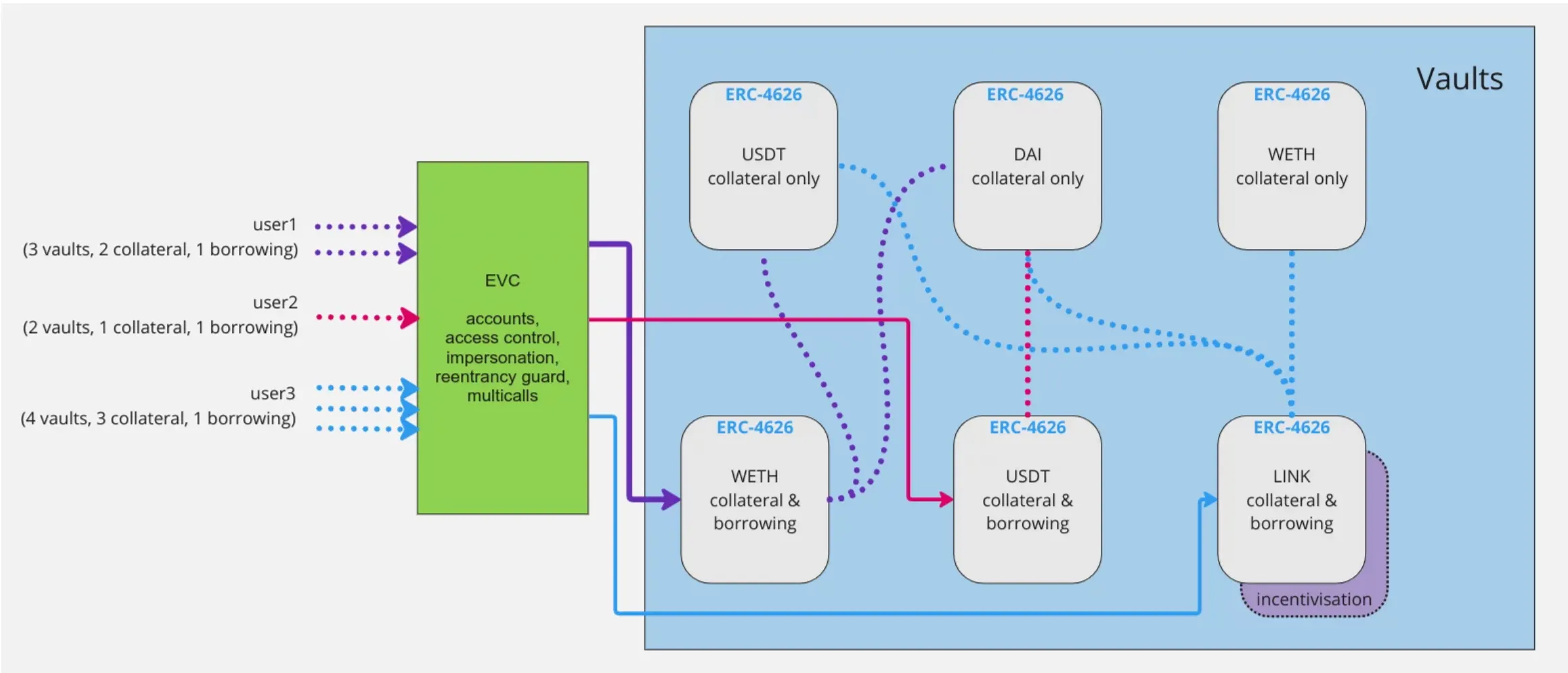
===

Health score#

To avoid to be liquidated, keep $HealthScore$ greater than 1.0 .

Generally $HealthScore$ is denoted as

Evaluate risk-adjusted collateral#

Here assume a user deposit a single asset and leverage its position.

Let $a^c$ denote the balance of collateral and $s^c$ denote the self-collateralized balance of collateral. Let $f^c$ denote the collateral factor of a asset, $f^b$ denote its borrow factor and $f^s$ denote the collateral factor of a self-collateralized asset (called self-collateralized factor).

Risk-adjusted collateral is calculated as

where $f^c \leqq f^s$.

References#

https://github.com/euler-xyz/euler-contracts/blob/6086c6e585f03ceb3365a4e011dc892af96f1de8/contracts/modules/RiskManager.sol#L317-L329

Evaluate risk-adjusted liability#

Risk-adjusted liability is calculated as

where self-collateralized part of any asset have always 1.0 borrow factor. $s^b$ is always equal to $s^c$ ??

In Euler self-collateralized part of any asset has always 0.95 collateral factor and 1.0 borrow factor.

for example,

deposits 1000 USDC and mints 9000 USDC. normal CF of USDC is 0.9

now collateral 10000 USDC and liability 9000 USDC.

so, risk adjusted collateral = (10000 - 9000/0.95) * 0.9 + 9000 * 0.95 = 9023
risk adjusted liability  = 9000*1

Peusdocode#

function getCurrentHealthScore() public view returns (uint256) {
        IMarkets.AssetConfig memory config = EULER_MARKETS.underlyingToAssetConfig(token);
        uint256 cf = config.collateralFactor;
        uint256 balanceInUnderlying = IEToken(config.eTokenAddress).balanceOfUnderlying(address(this));
        uint256 selfAmount = dToken.balanceOf(address(this));

        require(selfAmount != 0, "strat/no-borrow");

        // selfAmountAdjusted = selfAmount * CONFIG_FACTOR_SCALE) / SELF_COLLATERAL_FACTOR;
        uint256 riskAdjustedCollateral = (cf *
            (balanceInUnderlying - (selfAmount * CONFIG_FACTOR_SCALE) / SELF_COLLATERAL_FACTOR)) /
            CONFIG_FACTOR_SCALE +
            selfAmount;
        uint256 riskAdjustedLilability = selfAmount;
        return (riskAdjustedCollateral * EXP_SCALE) / riskAdjustedLilability;
}

Calculate the amount to mint or burn to maintain a target health score.#

Minting#

Let $h_{\text{target}}$ $>1$ denote the target health score we want to maintain.
Let $x$ denote its newly added collateral and $x^s$ denote its newly added collateral with recursive borrowing (eToken.mint()).

The strategy deposits its underlyings with $eToken.deposit(amount \, x)$ and $eToken.mint(amount \, x^s)$.

Resolve the equation for $x^s$.

Burning#

The strategy withdraws its underlyings with $eToken.withdraw(amount \, x)$ and $eToken.burn(amount \, x^s)$.

References#

https://github.com/euler-xyz/euler-contracts/blob/6086c6e585f03ceb3365a4e011dc892af96f1de8/contracts/modules/RiskManager.sol#L331-L334